How to Use Decision Trees in HR Analytics: A Practical Guide
While linear regression models have been the default tool used by many HR analysts, they are not always the best way to capture patterns in your HR data. Not all HR phenomena can be described by drawing straight lines. Here, more flexible, algorithmic modeling approaches like decision trees can form a valuable addition to an HR analyst’s toolkit.
Let’s have a look at how to use decision trees in HR analytics in detail.
Contents
What is a decision tree?
When to use decision trees in HR analytics
Terminology
Use case example
Building the decision tree
What is a decision tree?
A decision tree is a supervised machine learning algorithm that produces a non-parametric model. The supervised part means that the decision tree is built in situations where the values of both the independent and dependent variables are known. The non-parametric part implies that the decision tree model makes no assumptions about the underlying data distributions.
Decision trees are thus very flexible. They can even be used out-of-the-box for both classification (i.e., categorical outcomes) and regression (i.e., numerical outcomes) purposes.
Two leading developers are accredited for developing the decision tree algorithm: John Ross Quinlan and Leo Breiman.
Around 1984, Quinlan named his decision tree algorithm Iterative Dichotomiser 3 – or ID3 in short – and later developed variants C4.5 and the commercial C5.0. Breiman and his colleagues at Berkeley named their decision tree algorithm simply Classification and Regression Trees – or CART in short – and their implementation is most commonly used in practice.
In this article, we leverage the implementation of Breiman’s CART in the statistical programming language R.
If you want to boost your R skills for HR analytics, our People Analytics Certificate Program is a great place to start.
When to use decision trees in HR analytics
Decision trees are a great addition to your HR analytics toolbox. They easily find and leverage complex non-linear effects in your HR data and do so almost without the analyst’s involvement.
Decision trees are especially valuable in specific situations:
- When you have highly dimensional data (i.e., many variables) and you are not sure which have predictive potential. Here are a couple of examples:
- You have surveyed characteristics of team climate (work pressure, leadership style, feedback, autonomy, etc.) and are curious about the correlates of high employee turnover.
- You have many data points on employees’ career histories and are curious about the correlates of career progression (promotion).
- You have detailed data on your employees’ work experience (e.g., text data from CVs) and are curious about what correlates to hiring decisions.
- When your dependent variable is not normally distributed (e.g., skewed data like salaries or absence rates)
- Or when you expect non-linear effects, like higher-order polynomials or maybe interactions and moderating effects between variables, for example:
- You have surveyed characteristics of team climate (work pressure, leadership style, feedback, autonomy, etc.) and are interested in the situations/combinations in which you experience high employee turnover.
- You have many data points on employees’ career histories and are interested in the situations/combinations in which the most career progressions (promotions) occur.
- You have detailed data on employees’ work experience (e.g., text data from CVs) and are curious about which set of experiences may predict successful hires.
- You expect that there is a relationship between tenure and sales performance but that it is not linear. You expect low performance at the start, high performance during years 2 through 5, and then a slow decline.
Terminology
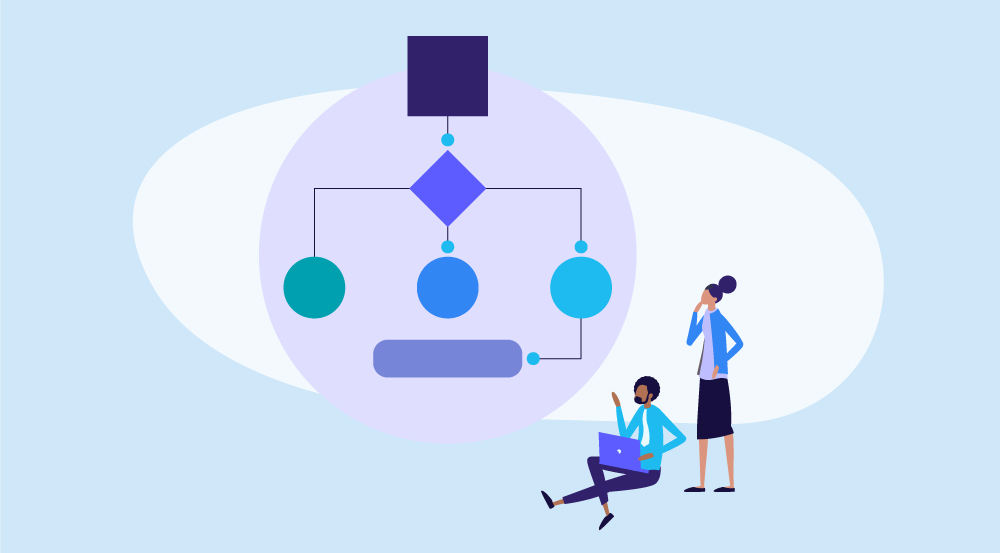
The main idea behind the decision tree algorithm is to represent data as a set of decision rules that form a tree-like structure.
Figure 1 below shows a decision tree, and you should read it from top to bottom. You start at the top with a root node. Each subsequent node in the tree is either a decision node – where data is split into subsets based on some condition – or a leaf node – where a data subset resides which is not split up further.
Each decision node forms a conditional test that results in a binary decision rule (yes/no), like “Is this employee a manager?”, “Is this employee a High potential?”, or “Does this team have more than six employees?”.
The resulting tree resembles a flowchart. Here, each node shows a conditional test for an independent variable (also called a feature); each branch shows the outcome of the test, and each leaf node shows a subset of HR data where the model estimates some average value or probability. The variables and cut-off values are chosen based on their added value for predicting/classifying the dependent variable (also called the target).
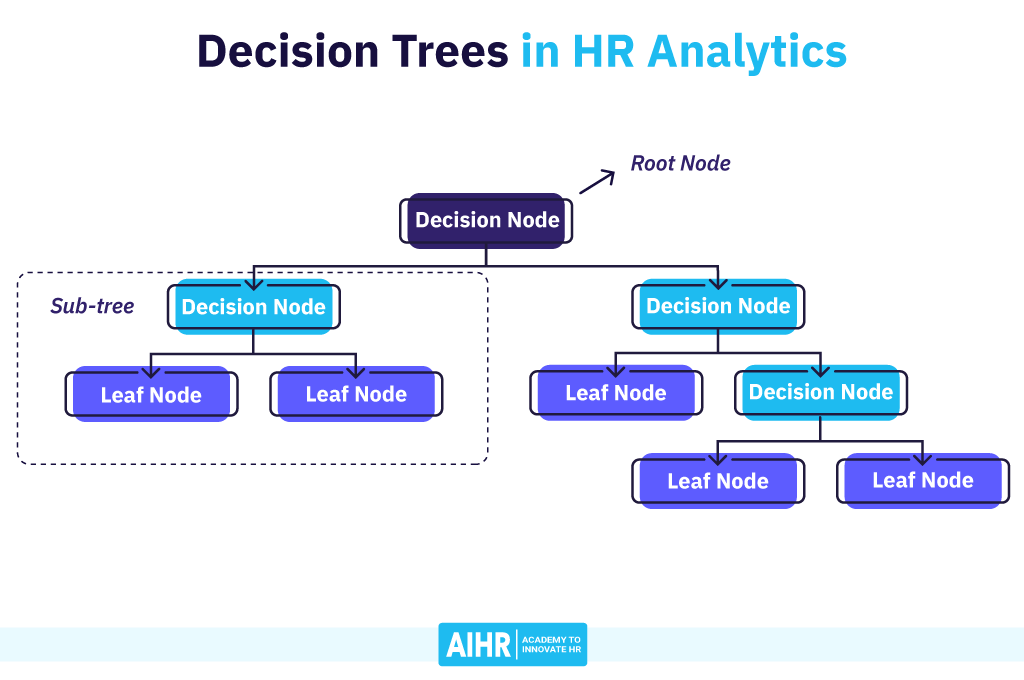
Figure 1: A conceptual drawing of a decision tree and the associated terminology. (Image source)
Use case example
Let’s see how these decision trees work.
In practice, you will probably use decision trees on large datasets. This is both in terms of the number of employees included, and the number of variables modeled. Yet, a small example helps to illustrate its inner workings.
We use the HR dataset shown in Table 1. It contains typical information you would find in your HR Information System and involves 18 employees.
Our data contains three independent variables: the job type, a potential assessment, and how many years have passed since the employee got their last promotion.
Our target is to predict the dependent variable turnover, indicating whether an employee has left the organization. This represents a classification problem, as we want to predict whether employees should be classified as “Yes” or “No” regarding their turnover.
Table 1: Example dataset with employee information taken from typical HRIS
Employee name Job type Potential Years since promotion Turnover Alfred Manager High 6 No Bojin Individual Contributor Low 6 No Corry Individual Contributor Medium 3 No Dennis Individual Contributor High 10 Yes Everhard Individual Contributor Low 2 No Finny Individual Contributor Medium 10 No George Individual Contributor Medium 6 No Herman Individual Contributor High 1 No Iuja Individual Contributor Low 7 No Jack Manager Medium 8 No Konstantin Manager Low 0 No Luis Individual Contributor Medium 4 No Maxime Individual Contributor Medium 1 No Nbusu Individual Contributor High 0 No Olav Individual Contributor High 5 Yes Pjotr Manager Medium 1 No Quirien Individual Contributor High 7 Yes Rodriga Individual Contributor High 6 Yes
The decision tree’s main objective is to split these employees into subgroups that have the “purest” separation of classes. This means that its leaf nodes should contain primarily employees who either all have “Yes”, or all have “No” on the target variable turnover.
Building the decision tree
The tree-building process starts with the full dataset of 18 employees at the root node of our tree. Here, no splits have yet been considered. Therefore, this node now contains 100% of the dataset. The employees in this node have an average value of 0.22 on the target variable or, in other words, 22% have a turnover value of “Yes” and left the company. This implies that the majority of this root node belongs to the non-turnover class (“No”), so this is the value that our decision tree predicts for all employees in this node.
The decision tree algorithm now needs to find the decision rule that best separates the two classes. Hence, it iterates to split these employees into subgroups in all possible ways. All possible cut-off values for each of the three independent variables in our dataset are examined and evaluated.
Starting with the variable Job type, the algorithm encounters two unique values – Manager and Individual Contributor. This presents two identical ways to split the data, separating all managers from non-managers or all individual contributors from non-individual contributors.
For the variable Potential, three splits are possible, isolating employees with either Low, Medium, or High potential from their colleagues.
For numerical variables, the decision tree first extracts the set of unique values. Next, it computes the mean for every pair of two subsequent values. These mean values are used as cut-offs, where the decision tree separates employees who score lower from those who score higher than the cut-off. Therefore, for the variable Years since promotion, the decision tree examines a total of seven splits for the cut-off values of 2, 5, 7, and 9.
Overall, Table 2 shows the total of nine ways to split our HR dataset at the root node.
Table 2: All possible splits at the root node, sorted by Gini impurity (see below).
Decision rule Gini Impurity Potential == High 0.190 Potential == Medium 0.283 Job type == Manager 0.317 Job type == Individual Contributor 0.317 Potential == Low 0.317 Years since promotion < 2 0.317 Years since promotion < 7 0.321 Years since promotion < 9 0.326 Years since promotion < 5 0.331
The decision tree algorithm needs to quantify how good each of these splits is to find and use the best split. There are multiple criterion metrics to determine the goodness of a binary split, but the most commonly used one is Gini impurity.
Gini impurity measures the average probability of mislabeling an observation when using a random label drawn from the current set of labels. That may sound complex but actually works quite intuitively.
When all randomly drawn labels would be correct, the Gini impurity is 0. This is the minimum Gini value possible, and it only occurs in pure nodes – like a subgroup of employees who all score “Yes” on turnover. In these pure nodes, any randomly drawn label from such a homogenous subgroup would be correct.
In subgroups where there are as many employees belonging to the turnover class “Yes” as belonging to “No”, you would get a Gini impurity of 0.5. Here, only half of your randomly drawn labels would be correct. In sum, a low Gini impurity reflects a more homogenous subgroup, which is what the decision tree looks for. It seeks to find decision rules that result in accurate predictions.
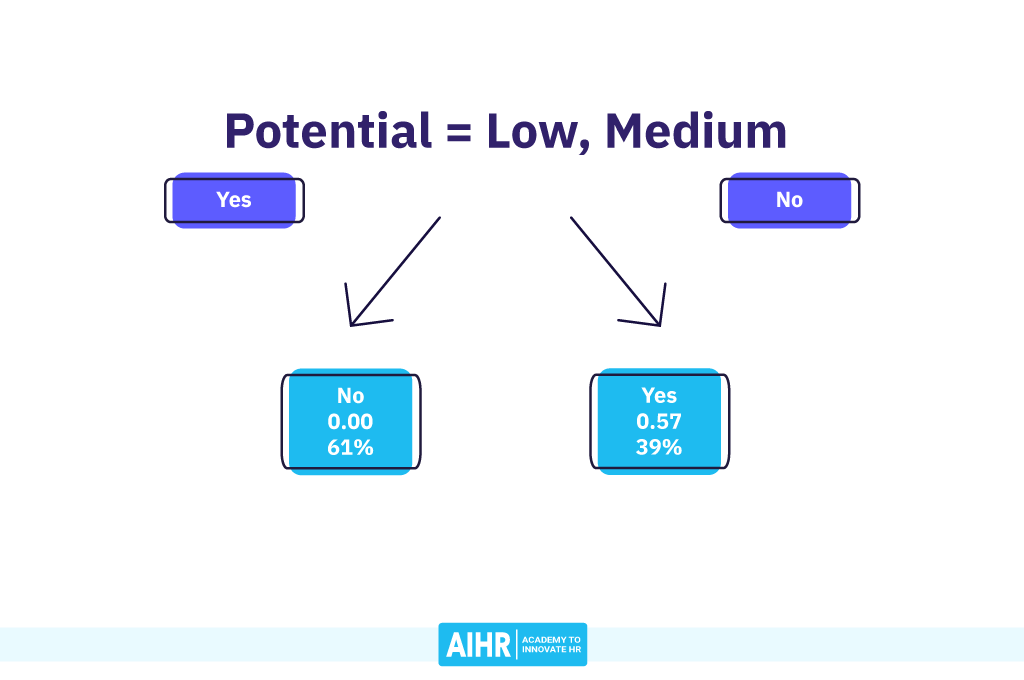
The tree finds the best split by using the decision rule that results in the lowest Gini impurity. Potential == High split produces the lowest Gini impurity (.190) and thus the best separation of turnover cases from retained employees. Hence, this decision rule is performed at the root node in Figure 3, although it’s named differently by our program.
This produces two branches with associated nodes. All employees with Low and Medium Potential are assigned to the left node, representing 61% of the total dataset. None of them turned over, so this is a pure node. This, among others, caused the low Gini impurity for this decision rule. As the proportion of turnover in this node is 0.00, the decision tree predicts “No” for all observations.
The right-hand node now contains all employees with High Potential. This represents 39% of the dataset. The proportion of turnover here is 0.57 or 57%, and thus the decision tree predicts this groups’ turnover to be “Yes”.
Being a pure node, the decision tree no longer considers further splits for the left-hand node. This left node can thus be considered a leaf node.
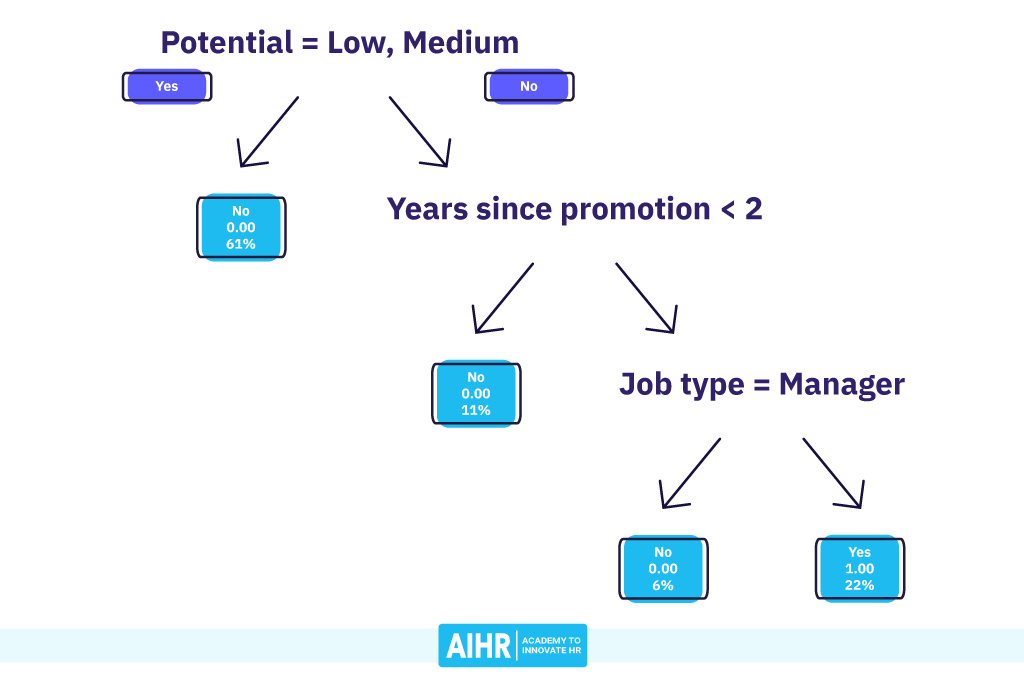
The decision tree algorithm repeats the same process for the right-hand node. It computes the Gini impurity of all possible splits (Table 3) and selects the decision rule producing the lowest Gini impurity (see Figure 4).
Table 3: All possible splits at node 3 — containing all High Potential employees — sorted by Gini impurity
Decision rule Gini Impurity Years since promotion < 2 0.229 Years since promotion < 7 0.343 Job type == Manager 0.381 Job type == Individual Contributor 0.381 Years since promotion < 5 0.405 Years since promotion < 9 0.429
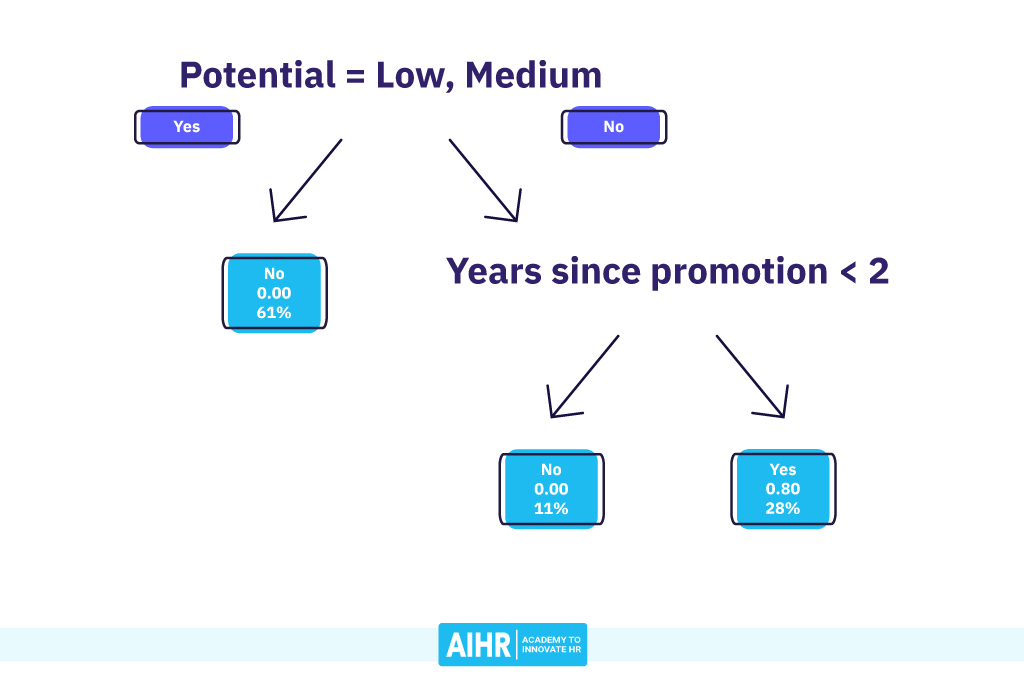
At this point, the split by Years since promotion smaller than 2 best separates the remaining turnover cases from the employees who stayed. Again, a pure leaf node appears on the left-hand side (node 4), containing all High Potential employees promoted in the last two years. These two employees (11% of the sample) show a 0% probability of turnover.
Node 5 on the right-hand side contains all High Potential employees who have been waiting for a promotion for two years or longer (28% of the sample). They show an 80% probability of turnover.
Because node 5 is not pure yet, further splits might be possible for the decision tree to consider. We will skip the Gini details for now, but Figure 5 demonstrates the next best separation, based on whether the Job Type is Manager. If so, they end up in the left-hand side node 6, which, again, is a pure node with 0% turnover. Similarly, node 7 on the right-hand side is also pure, with Individual Contributors who all turned over.
Our decision tree is now complete, with all final nodes considered leaf nodes. Through three simple rules, our decision tree was able to separate all turnover cases from their retained colleagues. Moreover, it was able to capture two interesting non-linear patterns. Time in position (i.e., years since promotion) was only relevant for the turnover of High Potential employees, and only for Individual Contributors, not for Managers.
A final word
You witnessed how decision tree algorithms form a great addition to an HR analyst’s toolbox. They allow for the flexible and easy discovery of complex patterns. Moreover, the output models are intuitive to understand and explain to others – even non-technical stakeholders.
While decision trees definitely come with limitations, we feel that the HR domain has a lot to gain from the more widespread use of these “machine learning” algorithms.
Weekly update
Stay up-to-date with the latest news, trends, and resources in HR
Learn more
Related articles
Are you ready for the future of HR?
Learn modern and relevant HR skills, online